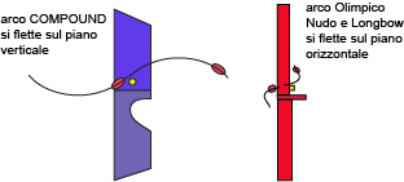
Lo si può definire scherzosamente, “ WOW”, la freccia compie evoluzioni che sembrano impossibili, eppure vedendo i filmati in Slow-motion che alcune macchine fotografiche realizzano, restiamo incantati a vedere cosa succede. La freccia per gli archi Olimpici, Nudi e Longbow, serpeggia sul piano orizzontale, mentre per gli archi Compound, ondeggia sul piano Verticale, l’importante è che i nodi della freccia restino allineati. Il paradossi del filosofo Zenone, circa 450ac. : Il paradosso è una proposizione formulata in apparente contraddizione con l’esperienza o con i principi elementari della logica, ma che all’esame critico si dimostra valida. Il termine, infatti, deriva dal greco paràdoxos che significa, appunto, “contrario alla comune opinione” e si differenzia da antinomia, anch’essa una parola di origine greca, il cui significato è, invece, “contro la legge” e, quindi, “contraddizione”. Come impostazione, il paradosso è stato molto spesso utilizzato, fin dai tempi antichi, per dimostrare tesi apparentemente assurde che richiedevano una spiegazione più complessa di un normale procedimento logico. Molte volte, tesi di questo genere avevano proprio a che fare col concetto di infinito. Esso, infatti, in quanto difficilmente comprensibile e accettabile dalla mente umana, ha sempre stimolato ragionamenti particolari e complicati. Per quanto riguarda l’antichità, i paradossi sono riscontrabili nella filosofia di Zenone (V secolo a. C.), appartenente alla scuola Eleatica. Per gli antichi, abituati ad un’osservazione superficiale della realtà, l’infinito era un concetto praticamente